11 Container With Most Water 1
Joel Castillo Espinosa 2
DESCRIPTION
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the $i^{th}$ line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
Examples
Fig 1. Diagram for example 1
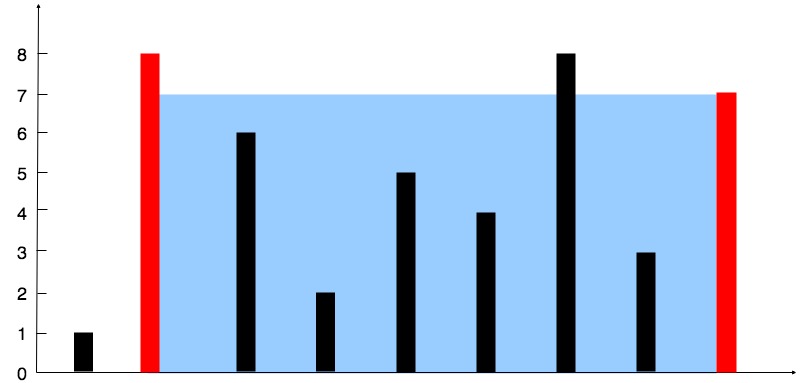
- Example 1:
- Input: height = [1,8,6,2,5,4,8,3,7]
- Output: 49
- Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
- Example 2:
- Input: height = [1,1]
- Output: 1
Constraints:
- $n = height.length$
- 2 ≤ n ≤ $10^{5}$
- 0 ≤ height[i] ≤ $10^{4}$
SOLUTION 3
container <- function(height, n){
maxarea <- 0
for (i in 0:max(height)) {
# in each iteration, the height increase by 1
# for this height keep the columns that are >= (save in vector ind)
ind <- grep(TRUE, height >= i)
# if at least 2 columns in vector ind -> calculate the max area
if(length(ind) >= 2) {
# for a fixed height, the max area is calculated with the two columns
# more distanced (max width: the first and last element in vector ind)
# the max area is height*width
area <- i*(ind[length(ind)] -ind[1])
} else {area <- 0} # otherwise max area is 0
# comparing the max area with the calculated area
if(maxarea <= area){
maxarea <- area
}
}
return(maxarea)
}
Examples using the function
We can use the examples presented before.
container(c(1,8,6,2,5,4,8,3,7))
## [1] 49
container(height = c(1,1))
## [1] 1
-
This problem is originally from LeetCode, you can find it in Leetcode. ↩
-
Email: jocastillo@colmex.mx. For more content visit my website: https://joelcastillo.netlify.app
If you have any questions or suggestions, I’d be grateful to hear from you. ↩ -
This solution is entirely my own work. It was developed using R version 4.4.1 (2024-06-14 ucrt). ↩